Table of Contents
HTML offers some semantic tags that help add meaning to our content. Whenever possible use these tags to help search engines and browsers understand the structure of your page. Let's look at some of these semantic tags like article, section, aside, header, nav and footer.
Articles and Sections
They still make these, right?
You can think of an article as standalone content. Like in articles you might see in a newspaper, articles will ideally contain sections like introductions, the main content, and then perhaps a footer with some closing notes. You can also think of an article as a collection of sections. For example, you might have an article that contains a section for the introduction, a section for the main content, and a section for the closing notes.
Let's see an example:
HTML<!DOCTYPE html>
<html>
<head>
<title>Article</title>
</head>
<body>
<article>
<section class="header">
<h1>Article heading</h1>
<p>Hello there!</p>
</section>
<section class="main">
<p>This is the main content</p>
</section>
<section class="footer">
<p>Good-bye!</p>
</section>
</article>
</body>
</html>
As you can probably tell, section tags are used to split up the article into smaller, more cohesive parts. section tags act like div tags in that they're both blocks, but section tells the browser that whatever is inside is just a piece of the larger puzzle.
We used section tags for headers and footers, but there are actually tags made specifically for this.
Header and Footer tags
HTML<!DOCTYPE html>
<html>
<head>
<title>Article</title>
</head>
<body>
<article>
<header>
<h1>Article heading</h1>
<p>Hello there!</p>
</header>
<section class="main">
<p>This is the main content</p>
</section>
<footer>
<p>Good-bye!</p>
</footer>
</article>
</body>
</html>
The header tag defines the header of an article or section, while the footer tag defines the footer.
Asides
If you find yourself wanting to go into a bit of detail about the topic at hand, like for example a quick little snippet, use the aside tag. It's a little bit like a section tag, but it's not a block.
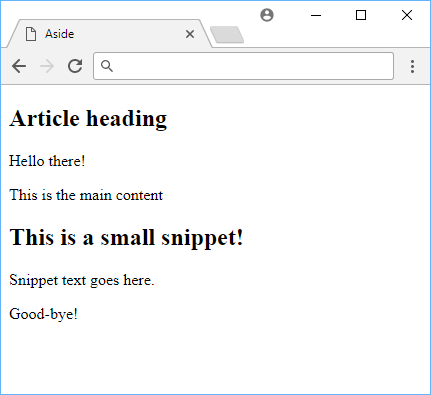
HTML<article>
<header>
<h1>Article heading</h1>
<p>Hello there!</p>
</header>
<section class="main">
<p>This is the main content</p>
<aside>
<h2>This is a small snippet!</h2>
<p>Snippet text goes here.</p>
</aside>
</section>
<footer>
<p>Good-bye!</p>
</footer>
</article>
The magic isn't something you can see visually!
Navigation
To more semantically define where your user can find navigation on your site, take advantage of the nav tag. Surround the links used for navigation with this tag and you're good to go.
HTML<!DOCTYPE html>
<html>
<head>
<title>Navigation</title>
</head>
<body>
<nav>
<ul>
<li><a href="/page1">Page 1</a></li>
<li><a href="/page2">Page 2</a></li>
<li><a href="/page3">Page 3</a></li>
</ul>
</nav>
<article>(Article content here)</article>
</body>
</html>
Semantic tags can be a powerful way to help your users find what they're looking for.
Resources
Getting Started with Express
Create an RSS Reader in Node
Getting Started with Electron
How to build a Discord bot using TypeScript
How to deploy an Express app using Docker
How to deploy a Node app using Docker
Learn how to build a Slack Bot using Node.js
Creating a Twitter bot with Node.js
Building a Real-Time Note-Taking App with Vue and Firebase
Getting Started with React
Setting Up Stylus CSS Preprocessor
How To Create a Modal Popup Box with CSS and JavaScript